Позитивные и негативные тесты для синтаксического анализатора

В данной работе парсером мы называем булевскую функцию, заданную на множестве последовательностей токенов и принимающую значение “истина”, если последовательность является предложением данного формального языка, и “ложь” – иначе. Конечно, реальные парсеры могут иметь дополнительную функциональность (например, помимо булевского значения выдавать дерево разбора или идентификацию ошибки), но здесь мы такую функциональность не рассматриваем.

Позитивный тест для парсера – это последовательность токенов, на которой парсер выдает вердикт “истина”, т.е. последовательность токенов, являющаяся предложением целевого языка.

Негативный тест для парсера – это последовательность токенов, на которой парсер выдает вердикт “ложь”, т.е. последовательность токенов, не являющаяся предложением целевого языка.

Для построения какого-нибудь позитивного теста достаточно, следуя правилам грамматики и ограничив рекурсию правил, вывести из стартового символа некоторую сентенциальную форму, состоящую из одних токенов. При построении же негативных тестов возникают два вопроса: насколько произвольна должна быть соответствующая последовательность токенов, и как добиться того, чтобы она действительно не принадлежала целевому языку. Сначала ответим на второй вопрос: как получить последовательность токенов, гарантированно не принадлежащую множеству предложений целевого языка.

Рассмотрим грамматику G= (T ,N,P,S). Для каждого грамматического символа X ?T ?N, определим множество UX вхождений символа X в грамматику G. Это множество состоит из всех пар

(правило p ?P, номер i символа в правиле p)

таких, что символ, стоящий на i-ом месте в правой части правила p является грамматическим символом X. Пару (p,i) ?UX будем называть вхождением символа X в правило p.

Пусть t – токен. Для каждого вхождения u ?Ut, u = (p,i), p = X > ?t? токена t в грамматику G можно построить множество Fu токенов t'?T таких, что существует вывод

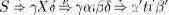
Здесь греческие буквы обозначают некоторые субсентенциальные формы, т.е.
последовательности нетерминалов и токенов. Если в грамматике G существует вывод S

?? t предложения, оканчивающегося токеном t, то будем считать, что множество Fu содержит пустую последовательность ? ?Fu. Через Ft будем обозначать объединение множеств Fu для токена t:

Иными словами, множество Ft – это множество токенов, каждый из которых допустим для токена t в качестве следующего. В дальнейшем нас главным образом будет интересовать дополнение к множеству Ft в множестве T ?{?}. Будем обозначать это дополнение через

Теорема 1. Последовательность токенов, содержащая подпоследовательность tt', где t'?

t, не является предложением языка, описываемого грамматикой G. Доказательство. Очевидно из построения множества

t. > Для последовательности токенов ? = t1...tn такой, что существует вывод S

???, можно определить множество токенов

такое, что если t'?

, то не существует вывода S

??t'?. Тогда любая последовательность ??t'?, где t'?

, не является предложением языка, описываемого грамматикой G. Итак, мы научились получать последовательности токенов, заведомо не являющиеся предложениями целевого языка. К вопросу о произвольности негативной последовательности токенов мы вернемся в следующем параграфе.

Содержание раздела